Question 1
The following table shows the number and rate of deaths due to transport accidents and assaults for young Australians.

With respect to young Australians in 2004, which of the following can be best concluded from the table above?
- A transport accident is a more common occurrence than an assault.
- About 25% of the persons aged 18-24 dying from a transport accident were female.
- 0.093% of females aged 18-24 died as a result of a transport accident.
- Transport accidents and assaults are a major cause of death amongst the young Australian cohort.
Questions 2-5
This unit describes a process for creating a number sequence.
A Szabo sequence is created by finding the sum of the digits of a whole number, then adding this sum to the whole number to get the next term in the sequence.
For example, the next term after 403 is 410, since 403 + (4 + 0 + 3) = 410.
By repeating this process, we get successive terms of the sequence:
403, 410, 415, 425, 436, 449 ...
In this sequence, 410 is referred to as the term immediately prior to 415.
Any whole number can be used as the first term, or seed number, of a Szabo sequence. The seed number of the standard Szabo sequence is 1:
1, 2, 4, 8, 16, 23, 28, 38, 49, 62...
Question 2
Each of the numbers from 91 to 95 inclusive is used as the seed number of five different Szabo sequences.
The three seed numbers which produce sequences that have 107 as a member are
- 91, 92 and 94.
- 91, 94 and 95.
- 91, 92 and 95.
- 92, 94 and 95.
Question 3
What is the sum of the digits of the term immediately prior to 704 in a Szabo sequence?
- 11
- 15
- 18
- 19
The following additional information refers to questions 4-5.
Some numbers only appear in Szabo sequences if they are the seed number, because no number can immediately precede them.
For example, we can prove that 53 has no term immediately prior to it.
A search for it starts in the low fifties, but because 50 — the smallest number in the fifties — is followed by 55, we won't be able to reach 53 from 50 or any larger number.
From the forties we find that 44 immediately precedes 52, that 45 immediately precedes 54, but that 53 misses out.
The largest number in the thirties, 39, is followed by only 51. No smaller number needs to be tried.
Therefore 53 has no term immediately prior to it, which means that 53 can appear in a Szabo sequence only as the seed number.
Also, there are numbers which have two different terms immediately prior to them.
For example, 505 can be reached from 500 and 491. This is called merging.
Any number which is not a multiple of three produces a Szabo sequence which eventually merges with the standard Szabo sequence.
Question 4
The Szabo sequence which has 64 as its seed number merges with the standard Szabo sequence at
- 115.
- 122.
- 127.
- 128.
Question 5
A merge graph shows the standard Szabo sequence in rectangles and other sequences in circles.
Which of these merge graphs correctly shows how a sequence containing 178 and another sequence containing 187 merge with the standard Szabo sequence?

Question 6
Computer Scientist: It is inevitable that a computer program will eventually be able to defeat a human opponent at chess every time they play. Current computers can plot out millions of move permutations every second, and future computers will have even greater computational power. Humans, unable to match the computers' computational abilities, will not be able to prevail in a single match.
Chess Player: Your conclusion is incorrect. "While computers may possess vast computational abilities, they lack the capacity for insight and innovation demonstrated by all great chess players.
Which of the following can be best inferred from the statements of the chess player above?
- A computer with a capacity for insight and innovation could defeat any human player.
- Computers may defeat all human chess players consistently, but they are unable to enjoy either the game or the victory.
- Even the best computer chess programs are limited by the abilities of their programmers.
- Computational power alone is not sufficient to win consistently at the game of chess.
Questions 1-3
Rob invited his parents for a weekend to visit him and his new fiancee, Helen, as well as to meet her parents. Helen insisted on cooking a meal for them all, however after a few hours waiting, it became clear they were not coming and Helen's parents departed. Having just rang his parents, Rob returns downstairs to the kitchen.
Rob: You're not going to throw that away are you? Be a shame if it went to waste.
Helen: Dunno, I could probably use it in a stir-fry or something.
Rob: Good. Hey, come on Helen – worse things have happened. Let’s clear everything away and flop down on the sofa with a bottle of wine. God knows, we've got enough of it.
Helen: You're really going to pretend nothing's happened? Don't you think we should talk about this? You haven't even told me what they said on the phone.
Rob: How am I pretending? I just don't want to dwell on it. You can see what my parents are really like now and how we're clearly better off without them in our lives.
Helen: People don't just not turn up Rob...That's really odd. Were they ever even coming? I didn't invite them, I don't know what they said on the phone! I thought you had started to patch things up?
Rob: Look, Helen, I booked a hotel room...of course I thought they were coming. Did you think I didn't? Maybe you think I didn't even invite them? That I let you drag your Mom and Dad over here all so I could make a complete fool of myself
Helen: No, no, of course not...I'm just trying to understand. Did something happen?
Rob: It really doesn't concern you Helen.
Helen: Of course it concerns me, they're going to be my family too soon! Rob – don't walk away!
Rob: Alright look, it was my Dad ok? He's the one who refused to come and Mom being Mom just kow-towed to him. He's a bully Helen, that's all he is. And if he can't have things his own way...why do you think I moved to Canada?
Helen: I don't know. I thought.
Rob: I could have stayed on the farm, he wanted me to, but I knew I'd never be good enough! I captained my Rugby team, I did the subjects he wanted, I got married far too young just to please him.
Helen: But what about your Mum? Surely she can stand up to him?
Rob: No no no, she's just as bad. Used to think she wasn't, but she is. I used to think that all the hen-pecking had just worn her down, but that was just an excuse. That's why I wasn't on the phone for very long just now. Informed me she wasn't allowed to speak to me, because he is still very disappointed in me. Well, if she didn't agree she could have gotten in the car and driven up here herself. The truth is, they are just nasty, bitter people.
Helen: Oh Rob...I'm sorry.
Rob: So there you are, that's my parents. Can you blame me for not wanting to inflict them on you?
Helen: It's alright Rob, you don't need to defend yourself to me. You have a new family now – me, Henry, my parents. If they don't like it, well, we can just manage without them!
Question 1.
Which of the following best describe the tone of Rob's comment 'God knows we've got enough of it'?
- Critical and bitter
- Wry and resigned
- Facetious and irked
- Pithy and amused
Question 2.
Which of the following best describe how Helen would have said the comment 'No, no, of course not...I'm just trying to understand. Did something happen?'?
- Defensively
- Questioningly
- Composedly
- Mollifying
Question 3.
Which of the following best describes Rob's attitude towards his mother?
- Angered by her failure to assert her own point of view in a more forceful way
- Disenchanted by continual disappointments he has endured at her hands
- Betrayed by the realisation that she has failed to show up at such an important occasion, to meet his fiancee and future parents in law.
- Disappointed at her not holding up their agreement without telling him in advance
Questions 4-6
The following passage is from a recent novel. It details a son as he prepares to tell his father some news.
Novel: The Street Sweeper by Elliot Perlman, 2011
"What's wrong?" William McCray asked his son. Charles was going to have to tell his father. He had no choice but to tell him but he decided to wait till he got him home and made him a drink. He was going to have to be quick on his feet and make something up to distract his father’s attention from the truth on the way home. He knew his father had had a nose for the truth all his life so it would be a mistake to say something too fanciful. He had to think fast. But he was having trouble coping with his own distress. As they walked from the campus to the apartment everything seemed a little surreal. He waved to some colleagues in the distance. There were some students walking down the street in the same direction as Charles and his father. If they were to strike up a conversation with them it might distract his father for at least some of the way home. But then the students might want to talk to Charles about the very thing he was trying to keep from him till they got home. The students had just acknowledged him with a wave. They were catching up.
Question 4.
William McCray asks "What's wrong?"" in a _____ manner.
- accusatory
- suspicious
- concerned
- innocuous
Question 5.
Charles is feeling
- desperate
- anxious
- pressure from his father
- distracted
Question 6.
It is likely that what Charles is about to reveal to his father is
- of importance
- very personal
- going to change his father's perception of him
- insignificant
Question 1
Select the picture that would most logically and simply be the next in the series

Answer is D
The dot on the top-right corner of the hexagon alternates between not moving and moving one corner anticlockwise. The dot on the bottom-left moves one spot anticlockwise the first turn, then two the next, this continues increasing by one each move. The arrow moves two and a half sides anticlockwise each time.
Question 2
Select the picture that would most logically and simply be the next in the series

Answer is E.
Solution: In this series there are 3 components, a black circle, a vertical line and a horizontal line. The vertical line and horizontal line appear to form a cross when they overlap in the same box, however their movements remain separate throughout the series. The black circle moves diagonally to the bottom right and back up to the top left again when it reaches the bottom right hand corner. It alternates between moving 1 position and two positions. This means that in picture 5 the black circle must be located along that diagonal at the intersection of row 3 and column 3. The vertical line alternates between moving two spaces down and two spaces left. The horizontal line alternates between moving two spaces left and two spaces down. Both lines end up in row 2 of column 3 in picture 5, forming a cross. Therefore E is the correct answer as it is the option that satisfies this pattern.
Question 3
Select the segment that would most logically and simply complete the picture

Answer: B
In each row, the left and right squares are superimposed onto each other to make one image. Then this image is rotated 90 degrees clockwise to give the middle square.
Question 4
Select the segment that would most logically and simply complete the picture

Answer is C
The outer shape of column B is determined by the difference in sides between columns A and C. For example in the first row; the shape in A1 has 4 sides minus 1 for the circle in C1 meaning the shape in B1 must have 3 sides (triangle). Therefore in B2 there will be no outer shape as the difference between the number of sides of two triangles is 0. The middle circle alternates between black and white, therefore the middle circle will be white.
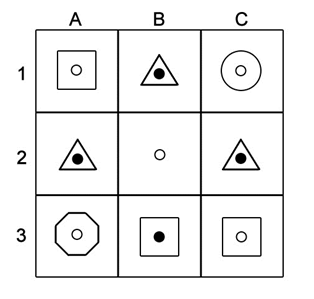
Question 5
The following figures can be arranged to form a logical sequence. Select the alternative (A, B, C, D or E) that most logically and simply fits in the middle of the sequence.

Answer: B
The sequence is displayed in the correct order (DABCE) below:

The number of sides of the black shape within the grid increases by 2 each move, from 6 to 8, 10, 12 and finally 14.
Question 6
The following figures can be arranged to form a logical sequence. Select the alternative (A, B, C, D or E) that most logically and simply fits in the middle of the sequence.
-

-

-

-

-

Answer: B
The correct sequence is AEBCD, as shown below

One grey triangle moves one quadrant clockwise, then two, then three and finally four quadrants clockwise. The other grey triangle alternates between the topmost and bottommost quadrants of the circle.
Both triangles alternate between pointing outwards and pointing towards the centre.